CS61B中的最小生成树问题

本教程总结CS61B 关于图章节中的最小生成树（Minimum Spanning Trees, MST）问题，以及对应的的算法

什么是最小生成树（MST）

考虑这样一个问题，给你一个无向图，你能不能找出这个图中的一组边，让其满足：

• 连通的
• 无环的
• 涉及到了所有的结点
  比如这样一张图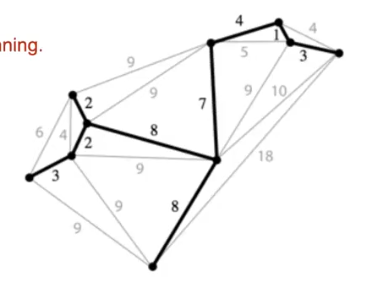
  
  这样的一组边构成的树，称为生成树
  而让这个树中所有的边权重之和最小即为最小生成树

如何找到最小生成树

一个非常有用的性质：割边属性（Cut Property）

• 一个 cut 就是将一个图中的结点分成两个非空集合
• 一个 crossing cut 就是从一个集合结点连接到了另一个集合结点的边
  割边属性是这样描述的：给定任意一个 cut，最小权重的 crossing edge 一定在最小生成树中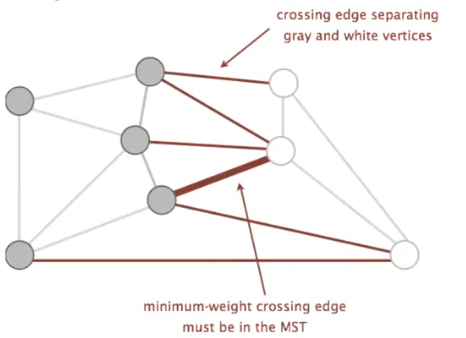
  
  比如上面这张图中，所有的红色边都是 crossing edge，其中最小的边一定在最小生成树中
  我们判断 crossing edge 只需要看这个边是否连接了两个属于不同集合（也就是不同颜色）的结点即可

通用的寻找 MST 算法

基于割边属性，我们可以这样构造一个算法：
首先一开始MST没有边：

• 找到一个没有 crossing edge 在MST中的 cut
• 然后将最小权重的 crossing edge 加入 MST
• 一直重复到 V-1 条边

Prim’s Algorithm

相比较最短路径树而言，最小生成树并不需要给出一个起点，在最小生成树中，只需要给你图然后说告诉我哪些边触及所有顶点且权重之和最小即可。

但是并不代表我们不选取一个起始结点，相对来说，Prim 算法会随机选择一个起始结点，这个随机性并不对最终结果产生影响（我们总要寻找一个结点来入手）

算法流程

从一个随机结点开始：

• 将一个一头连接已经在MST中结点的最短的边，加入MST,直到 V-1 条边

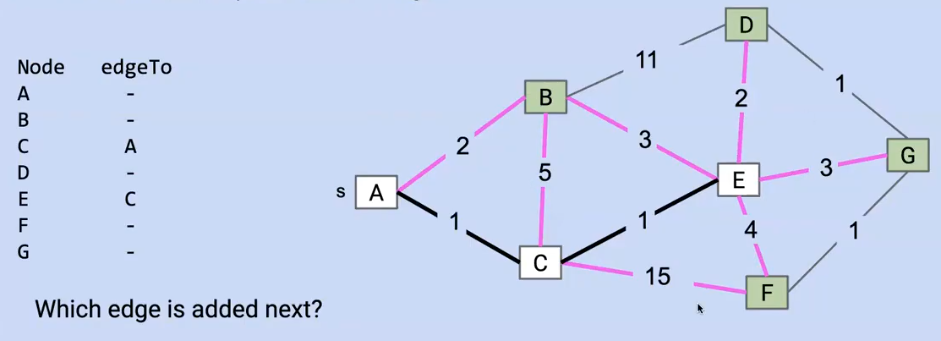
比如在这个图中，所有符合上述条件的即为红色的边：连接了一个在MST中的结点
然后我们选取这些边中最短的边，也就是A->B或者E->D

Prim 算法实际上是不断地使用了割边属性

改进的 Prim’s Algorithm

Prim 算法是可以奏效的，但效率太低了，因为你必须考虑大量的穿过这个 cut 的 crossing edge
我们对 Prim 算法进行改进：

• 将所有结点放入 fringe PQ 中，以结点到树的距离作为排序标准
• 重复：将距离树最近的结点移出，然后将其指出的所有边进行relaxation，然后对 distTo 和 edgeTo 数组进行更新

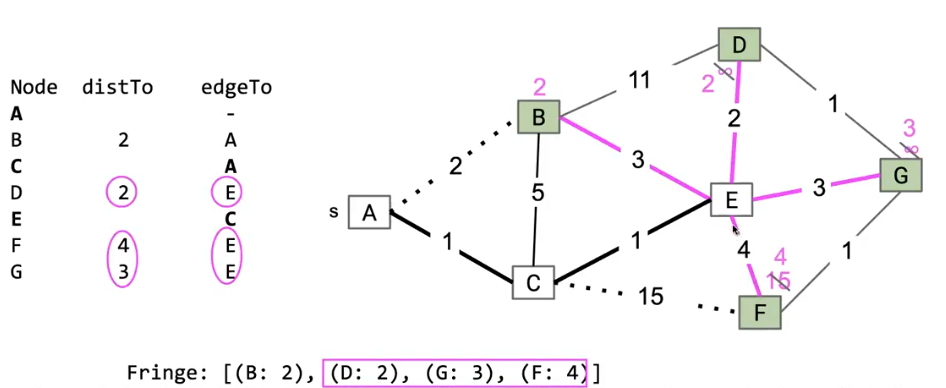
这个图中我们刚刚把距离树最近的结点E移出，加入到MST中，然后relax它的所有的边，同时更新 distTo 和 edgeTo 数组

图中加粗的边为MST中的边，图中的虚线表示relax出来的边，作为MST的候选边，如果在relax中发现这条边不如之前的边（比如C->B），或者这条边被后续的边所取代（比如下一步的C->F即将被E->F取代），那么这条边我们甚至不标注为虚线

而如果在MST中的边被新边取代，那么我们把新边加入MST，原来的边回到最开始的模样（不加粗，也不标为虚线）

同时我们看到 Fringe 中的结点是按照到树的距离进行排序的，同时 distTo 数组也变为了到树的距离

算法实现

public class PrimMST{
    public PrimMST(EdgeWeightedGraph G){
        edgeTo = new Edge[G.V()];
        distTo = new double[G.V()];
        marked = new boolean[G.V()];
        fringe = new SpecialPQ<Double>[G.V()];

        distTo[s] = 0.0;
        setDDistancesToInfinityExceptS(s);
        insertAllVertices(fringe);

        while(!fringe.isEmpty()){
            int v = fringe.delMin();
            scan(G,v);
        }
    } 
    ....

    private scan(EdgeWeightedGraph G, int v){
        marked[v] = true;
        for(Edge e: G.adj(v)){
            int w = e.other(v);
            if(marked[w]){
                continue;
            }
            if(e.weight() < distTo[w]){
                distTo[w] = e.weight();
                edgeTo[w] = e;
                pq.decreasePriority(w, distTo[w]);
            }
        }
    }
}

Kruskal’s Algorithm

按照权重顺序考虑所有的边，只要这条边加入MST后不构成环，那么就将它加入MST中，重复直到 V-1 条边

Kruskal 算法计算过程中创造出的MST可能是割裂不连续的，但是没关系，最后会得出正确的结果

我们可以通过维护两个辅助数据结构来帮助我们实现：

• WQU 加权快速集合：帮助我们判断是否有环生成
• MST ：统计最小生成树的边

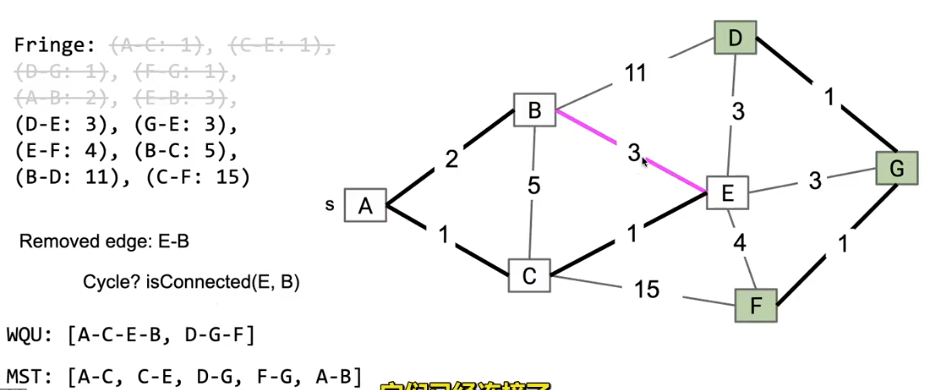
在这个图中我们按顺序从 Fringe 中取出对应的边，当我们即将取出E->B这条边时，WQU告诉我们已经有了一条从E到B的路径，也就是下一步即将成环，所以我们不考虑E->B这条边

算法实现

public class KruskalMST{
    private List<Edge> mst = new ArrayList<Edge>();

    public KruskalMST(EdgeWeighedGraph G){
        MinPQ<Edge> pq = new MinPQ<Edge>();
        for(Edge e: G.edges()){
            pq.insert(e);
        }
        WeighedQuickUnionPC uf = new WeighedQuickUnionPC(G.V());
        while(!pq.isEmpty()){
            Edge e = pq.delMin();
            int v = e.from();
            int w = e.to();
            if(!uf.connected(v,w)){
                uf.union(v,w);
                mst.add(e);
            }
        }
    }
}