logo
ZhangDas1
banner
The heap and heap sort in CS61B.

CS61B中的堆以及堆排序算法

Scroll down

本文章介绍 CS61B 中的堆(heap)，并介绍堆排序

什么是堆(heap)？

堆是一个在优先队列中表现良好的数据结构
虽然我们可以使用二叉搜索树(BST)，但是对于重复项，二叉搜索数就显得无能为力了

二叉最小堆(Binary min-heap)

二叉最小堆是一种完全的，并且满足最小堆性质的树：

  • 最小堆性质：每个结点都小于或等于其子结点
  • 完全：只有最后一层会不被填满，并且所有叶子结点都排布在左边

堆的好处

堆可以非常自然地实现优先队列的性质
比如一个简单的问题：你怎么支持getSmallest()这样一个方法呢
很简单，直接取出堆的根即可

堆的几个操作

添加结点

我们添加一个结点要同时满足堆的两个性质，也就是完全性和最小堆性，我们想一次性同时满足这两个性质是困难的。
所以我们可以先满足其中一个，然后对另一个做修正

比如：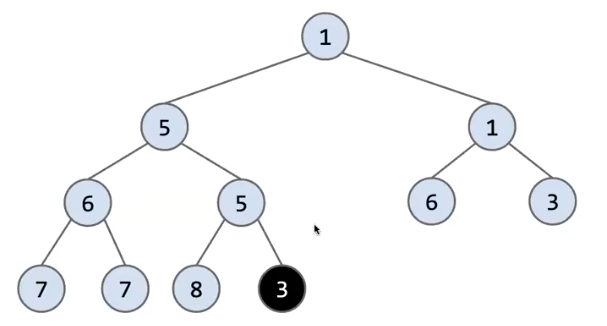
alt text
我在这个堆中添加一个 3 结点，首先我让其满足完全性，也就是把 3 结点添加到最左下角的部分

然后我们对这个最小堆性质做修正

  1. 3 的父结点 5 大于它，交换 3 和 5
  2. 交换后仍然 父结点为 5 ，继续交换
  3. 父结点为 1 ，满足最小堆

这个过程就像一个泡泡向上冒泡的过程，不断地与父结点做交换

删除结点

我们以删除根结点为例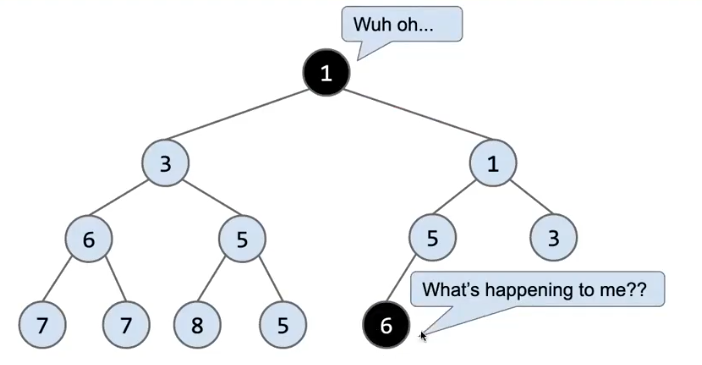
alt text
我们还是按照一样的思路，先满足完全性，再满足最小堆性质
我们想要删除根结点 1, 我们取“最后一个结点”，也就是最右边的叶子结点，将其放到根结点的位置
这个堆会变成这样：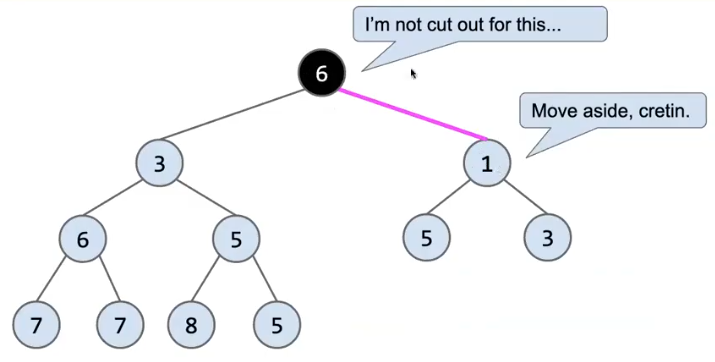
alt text

现在我们要逐步将其进行修正
现在这个根结点太大了，我们要将其逐渐“下沉”

  • 我们选取其子结点中更小的那个，然后将其交换
  • 不断重复，直到不再发生“下沉”

用堆实现优先队列

给我们一个堆结构，现在我们知道如何实现优先队列了

  • getSmallest()：返回根结点
  • add(x)：将新结点放在“最后一个位置”，然后进行“上浮”
  • removeSmallest()：删除跟结点，然后将“最后一个结点”放到跟结点，然后逐步“下沉”

如何在java中表示堆

得益于堆的完全性，我们知道，最后一层以上的所有层的结点数是有规律的：”1,2,4,8…”
如果我们按顺序对每个结点进行编号，我们可以写出parents[]数组
alt text
我们可以得到这样的求parent的方法：

1
2
3
public int parent(int k){
    return (k-1)/2;
}

我们可以把根结点放在索引 1 的位置，来简化方法表达
以此延伸我们可以得到

  • leftChild(k) = k*2
  • rightChild(k) = k*2 + 1
  • parent(k) = k/2

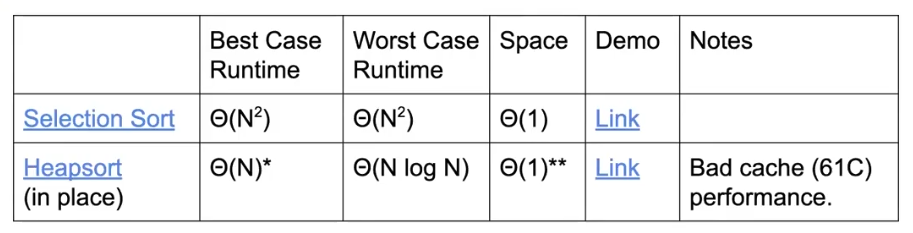
不同数据结构实现优先队列时间复杂度分析

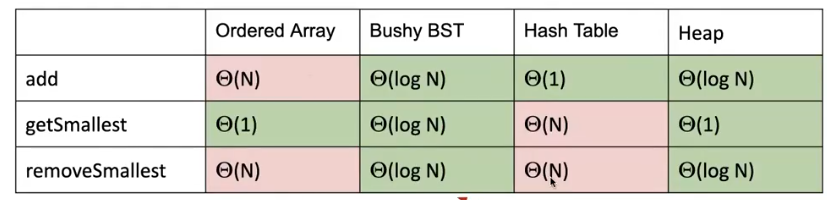
alt text
其中对于 Bushy BST 来说，如果有相同优先级的元素会很难处理

堆排序

选择排序

我们知道选择排序是每一次寻找数组的最小值，并把它放到已排序数组的前端
而我们知道堆排序具有第一个元素即最大/最小元素的性质，也就是getSmallest()或getBiggest()的时间复杂度为O(1)，由此得到堆排序

堆排序

初始想法

我们的初始想法是，将这个输入数组重排为一个最大堆，并用一个额外数组进行存储，再找一个额外数组作为输出数组，每次取出最大堆的第一个元素（根，即最大元素），放入输出数组的最后一个空位置。

改进思路

我们通过堆的性质改进了时间复杂度，但是我们还需要两个空间复杂度为O(N)的额外数组，我们不想要占用额外空间，我们可以怎么改进呢？

省去额外堆数组

但是我们发现，我们可以将输入数组就看作一个没有重排的堆，我们可以直接在这个数组基础上直接对它进行重排，将其构造为一个最大堆，这样我们就省去了一个额外存储堆的数组

省去额外输出数组

我们又发现，未排序的堆和已排序的堆的和总是为N，而且我们每次都是把最大值放到数组的末尾，我们可以将已排序的部分放在末尾，未排序的部分放在前面，每次重排都只重排未排序的部分，这样我们又省去了额外的输出数组的空间。

如何构造最大堆

对于最大堆，我们从后往前考虑（也就是从最后一层的最后一个向前考虑），对于每一个结点，都看其两个子结点是否小于自己，如果不，则进行交换
向上构造最大堆：

  • 按照逆序对每个结点进行下沉操作：sink(k)
  • 在下沉之后，保证以 k 为根的堆是最大堆

如何重排

我们每次取出根之后，进行重排，只需要执行sink(0)即可，这就让这个新上来的结点重新“下沉”下去了

算法流程

  1. 将初始输入看作一个堆
  2. 将初始堆构造为最大堆
  3. 重复
    1. 取出第一个元素（最大元素）
    2. 将其余元素前移（作为下一个初始堆），该元素放到已排序的前一个
    3. 其余元素重排为最大堆
  4. 直到全部已排序完毕

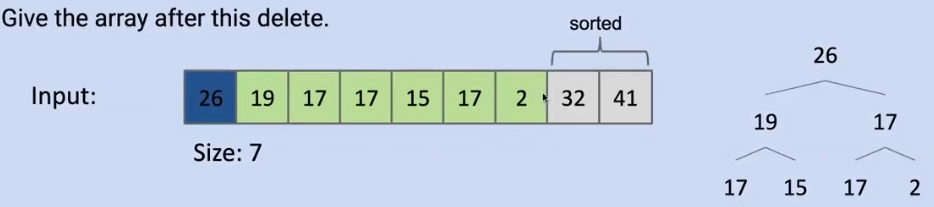
alt text
比如这个数组，我们每次选择第一个元素，将其放到末尾，然后对剩余元素进行重排，并重复这个操作即可

堆排序时间复杂度分析

  • 向上构造最大堆：O(N logN)——N 个结点每个执行sink为logN,即N * logN
  • 选择最大元素：O(1)
  • 移除最大元素并重排：O(log N)

堆排序与选择排序比较

alt text

其他文章
cover
Windows 中的常用命令
  • 25/07/23
  • 23:11
  • Ubuntu
cover
CS61B中的最小生成树问题
  • 25/07/21
  • 23:39
  • 数据结构
30+
Posts
8+
Diary
85+
fans
目录导航 置顶
  1. 1. 什么是堆(heap)？
    1. 1.1. 二叉最小堆(Binary min-heap)
  2. 2. 堆的好处
  3. 3. 堆的几个操作
    1. 3.1. 添加结点
    2. 3.2. 删除结点
  4. 4. 用堆实现优先队列
  5. 5. 如何在java中表示堆
  6. 6. 不同数据结构实现优先队列时间复杂度分析
  7. 7. 堆排序
    1. 7.1. 选择排序
    2. 7.2. 堆排序
      1. 7.2.1. 初始想法
      2. 7.2.2. 改进思路
      3. 7.2.3. 省去额外堆数组
      4. 7.2.4. 省去额外输出数组
      5. 7.2.5. 如何构造最大堆
      6. 7.2.6. 如何重排
      7. 7.2.7. 算法流程
    3. 7.3. 堆排序时间复杂度分析
    4. 7.4. 堆排序与选择排序比较