本教程介绍 CS61B 中的快速排序
快速排序
算法流程
- 选取一个**基准值(pivot)**,一般为最左侧的数字
- 将所有小于等于 pivot 的放在左侧,大于等于 pivot 的放在右侧
- 对于 pivot 左侧右侧的两个数组进行相同操作,重复
时间复杂度分析
每一次使用 pivot 进行基准划分之后,这个pivot已经被放置在了正确的位置,然后剩下的两个数组就相当于被分解为了两个子问题,直到被分解到 1 个数字的规模,则分解结束,那么我们知道,分解的越慢,则性能越差
我们知道,每次进行分解时,都是通过扫描数组,找出所有小于大于 pivot 的值,并放在对应的位置,所以这个按照基准进行分解的过程时间复杂度为 $\theta(N)$
最好情况
每次刚好都可以分解为两个相同规模的问题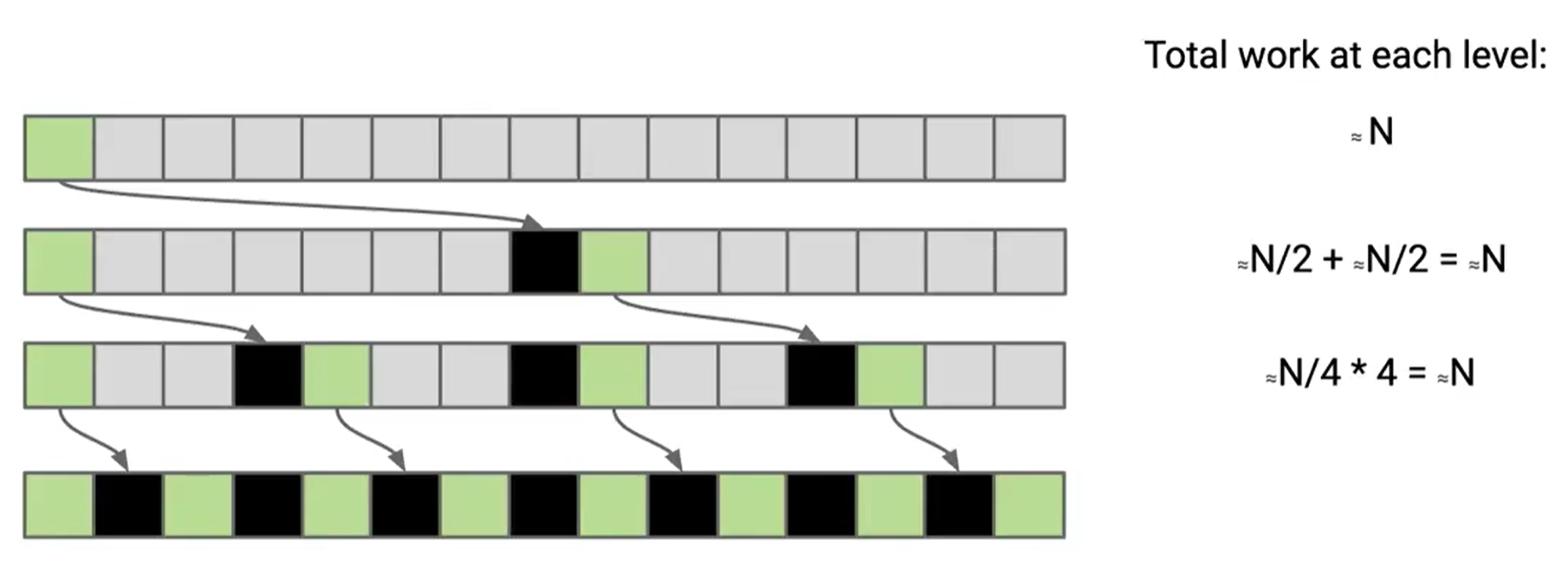
在这个图中,我们可以看到每次分解为两个相同规模的子问题,每次分解的时间复杂度为 $\theta(N)$,一共进行 $H=\theta(logN)$ 次分解,所以时间复杂度为 $\theta(NlogN)$
最坏情况
每次分解都只最小限度的分解问题,也就是分成了 0 和 N-1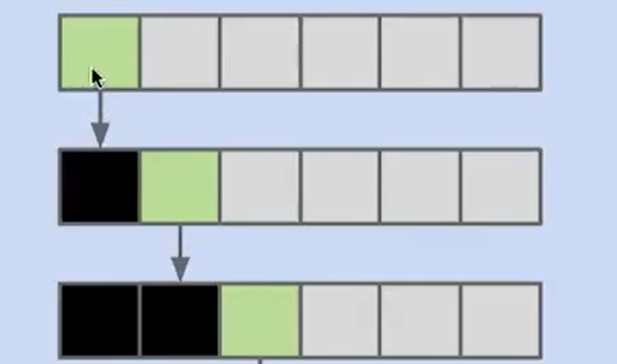
这样的话,我们一共要进行 N-1 次分解
那么时间复杂度为 $\theta(N^2)$
与归并算法的比较
理论上快速排序的分析:
- 最好:$\theta(NlogN)$
- 最坏:$\theta(N^2)$
归并算法: - 最好:$\theta(NlogN)$
- 最坏:$\theta(NlogN)$
但是实际上快速排序仍然是经验上来说的最快的算法,因为平均上来说,它的时间复杂度为 $\theta(NlogN)$,也就是任何随机数组,它的预期结果将是 $NlogN$
严格的证明需要可能性方法和计算,但是直觉和经验性的分析会很有希望说服你
论据
10% 情况
我们假设每一次分解 pivot 都会落到 10% 的位置,这样我们会得到两个不平衡的数组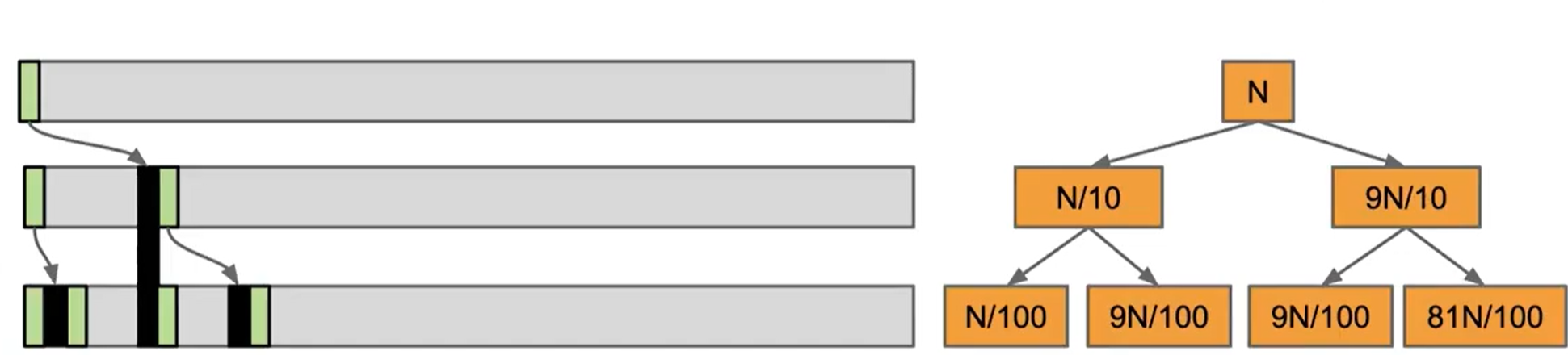
同样的在每一层,我们的时间复杂度都为 $O(N)$
而层数为 $H=log_{10/9}N=O(logN)$
我们发现总的时间复杂度仍然为 $O(NlogN)$!
快速排序与二叉搜索树(BST)
事实证明,快速排序实际上与二叉搜索树(BST)相同
BST 排序背后的想法是,获取所有元素,放入二叉搜索树中,然后中序遍历以获取排序数组
快速排序与BST的本质上是相同的,也就是它们进行的比较序列实际上是相同的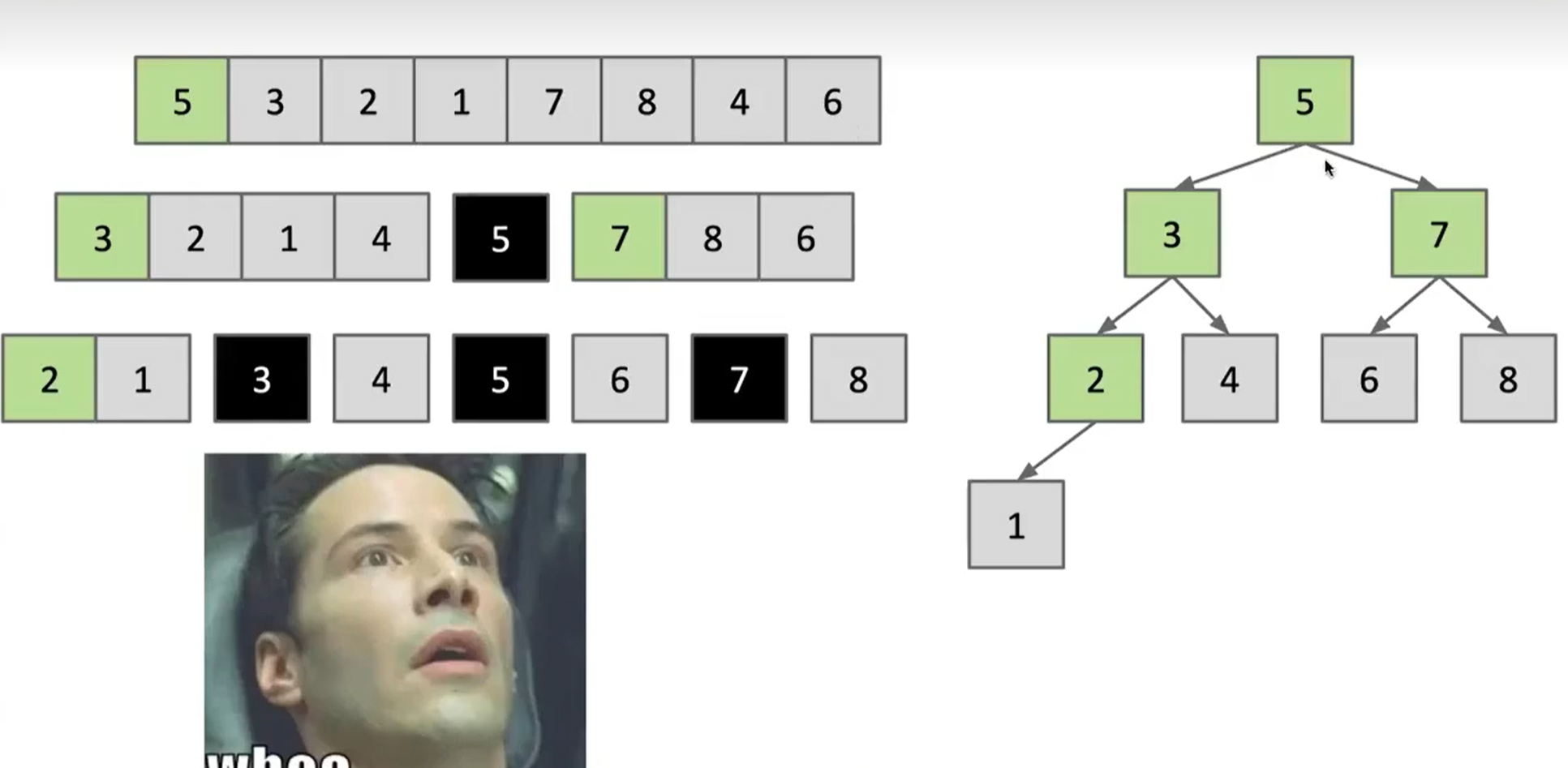
比如在这样一个数组中
- 选择 5
- 快速排序选择 5,然后让所有的数字与 5进行比较
- BST 选择5,也是剩下所有数组与 5 进行比较,因为 5 是根节点
- 选择 3
- 快速排序选择 3,剩下2、1、4与3进行比较
- BST 选择 3,剩下2、1、4与它进行比较
- …
同样的在BST中,最坏的情况是构建一个细长的树,而构建细长的树需要 $N^2$ 的时间,也就是 $NlogN$ (茂密的树)和 $N^2$ (细长的树)
避免最坏情况的表现
- 在快速排序之前打乱数组(避免对已排序数组进行快排)
- 扫描数组,找出中位数作为 pivot
- 扫描,检查其是否已排序,如果是,直接不排
四种哲学
- 随机性:随机选择一个 pivot 或者在开始之前进行打乱
- 更聪明的 pivot 选择:计算或者估计中位数
- 反省:如果递归太深,那么换一个更安全的排序
- 预处理:先分析数组是否适合快速排序
算法比较
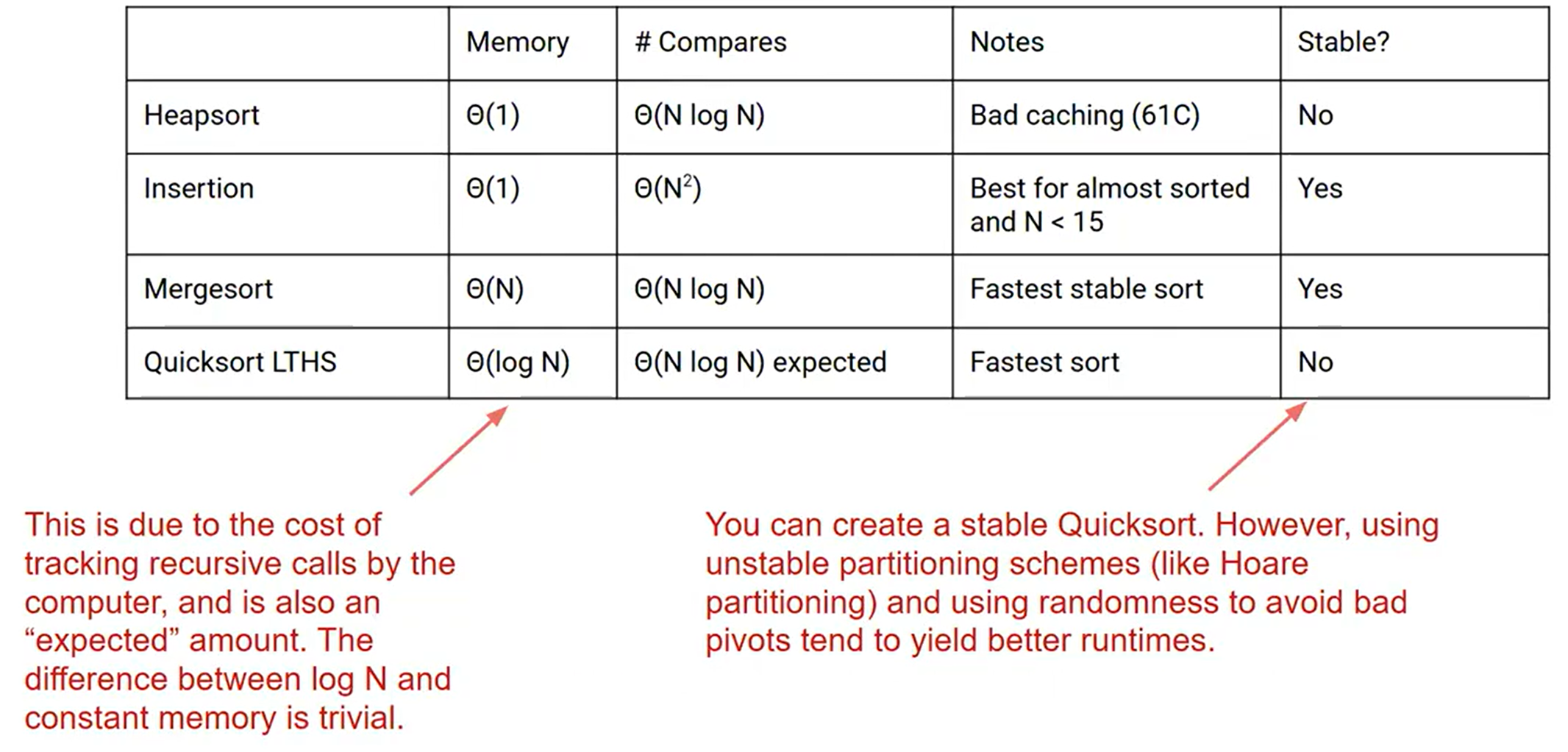
在这里快速排序的空间损耗是因为我们需要进行递归,而且这是一个预计值
而快速排序仍然是一个不稳定的排序,但是我们可以通过一些手段来使它变得稳定



